Par Philippe Cosentino
Contrairement à la modélisation « analytique » (qui repose sur la manipulation de variables, liées par des relations mathématiques), la modélisation par agents est abordable, intuitive, et accessible aux élèves dès le cycle 4.
C’est une approche particulièrement pertinente dès lors qu’il s’agit de modéliser les effets d’interactions entre des entités, que ce soient des organismes, des cellules ou des molécules, par exemple. En modélisant des comportements très simples, d’agents élémentaires, on étudie le fonctionnement de l’ensemble et on se laisse parfois surprendre par l’issue de la modélisation. C’est ce que l’on appelle une approche ascendante, « bottom-up », où l’on part du « bas », des entités élémentaires, pour faire émerger des propriétés plus complexes (l’ensemble intégré est en quelque sorte davantage que la simple somme de ses constituants).
Il était déjà possible, avant la conception d’Edu’modèles, de réaliser, ou de faire réaliser aux élèves de tels modèles, avec le logiciel « NetBioDyn » de Pascal Ballet, MdC à l’université de Brest. Edu’modèles a été construit sur la même base que NetBioDyn, mais présente un certain nombre de différences, que ce soit au niveau de l’ergonomie ou des fonctionnalités.
En quoi consiste la modélisation multi-agents ?
Un modèle multi-agents est composé :
- d’un environnement de type « grille » ou « damier »
- d’un certain nombre d’agents (ou d’entités), qui se déplacent de manière aléatoire sur l’environnement (quand ils ne sont pas immobiles)
- de règles définissant ce qui découle de la rencontre des agents
Les règles sont définies à la manière d’une réaction chimique : il y a des « réactifs » (les agents qui se rencontrent), et des « produits » (les agents issus de la rencontre).
On peut par exemple considérer la règle suivante :
renard + lapin → renard repu
Cette règle fait intervenir 3 types d’agents :
- renard
- lapin
- renard repu (qui est un agent différent de « renard »)
A l’issue de la rencontre, le lapin a disparu, et le renard est remplacé par un « renard repu ».
Créer un modèle multi-agents est aussi simple que cela. On commence par définir les différents agents peuplant notre environnement, puis on définit les règles régissant leurs rencontres.
Une fois le modèle construit, on l’exécute, on voit alors à l’écran les lapins et les renards se déplacer aléatoirement, et à l’issue de rencontre lapins-renards, on voit des lapins disparaître, et des « renards repus » apparaître.
Un graphique permet également de suivre dans le temps l’évolution des populations.
Comment réaliser un modèle multi-agents avec Edu’modèles ?
Vous trouverez sur ce site pédagogique académique divers exemples de situations à modéliser (les liens sont en bas de l’article).
Nous prendrons ici l’exemple suivant : nous souhaitons modéliser la catalyse enzymatique de l’hydrolyse du lactose par la lactase (bêta-galactosidase).
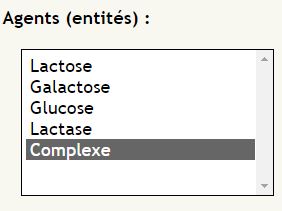
Tout d’abord nous devons énumérer les agents susceptibles de peupler notre environnement. A tout moment dans notre « récipient virtuel » (l’environnement), nous pouvons avoir :
- des molécules de lactose
- des molécules de glucose
- des molécules de galactose
- des molécules de lactase
- des complexes enzymatiques lactase-lactose
Il est inutile de modéliser l’eau, qui est omniprésente (tous les agents sont en permanence en contact avec de l’eau).
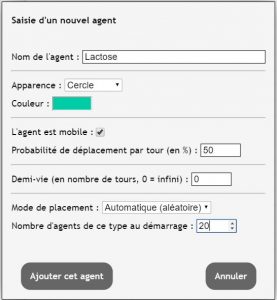
Pour créer ces agents, il suffit de cliquer sur « (+) Ajouter un agent » (à droite de l’écran).
Une fenêtre s’ouvre alors, et invite l’utilisateur à saisir un nom : on saisit « lactose ». On saisit également le nombre initial de molécules de lactose (par exemple 20). On peut également choisir la façon dont sera représenté l’agent : carré rouge, cercle bleu, image, caractère … à vous de choisir. Enfin on valide en cliquant sur « Ajouter cet agent ».
On fait de même pour les autres agents, en prenant garde de saisir la valeur zéro pour les molécules qui ne sont pas présentes au début de la réaction (galactose, glucose, et le complexe).
Reste à définir les règles modélisant les rencontres de ces agents. Elles sont au nombre de deux.
La première règle correspond à la rencontre entre l’enzyme et son substrat, on la modélise ainsi :
lactase + glucose → complexe
Attention, il ne s’agit pas d’une équation chimique, mais d’une façon de représenter ce qu’il advient à l’issue de la rencontre entre une molécule de lactase et une molécule de glucose.
Pour créer cette règle, on clique sur « (+) Ajouter une règle ».
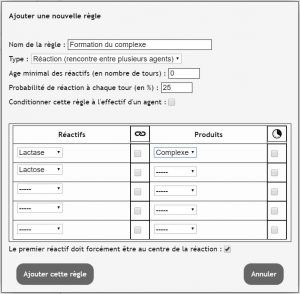
On est invité à saisir un nom, saisissons par exemple « Formation du complexe ».
Dans la colonne de gauche (réactifs) on sélectionne lactase, et lactose.
Dans la colonne de droite (produits) on sélectionne complexe.
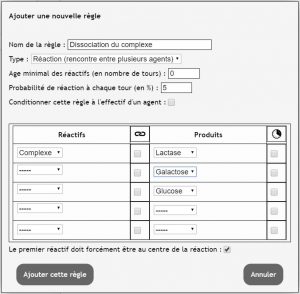
La deuxième règle modélise la dissociation du complexe.
complexe → lactase + glucose + galactose
Il n’y a qu’un seul agent qui intervient : le complexe. Il se dissocie spontanément en libérant l’enzyme, le glucose et le galactose. Pour éviter que cette dissociation ne se fasse immédiatement après la rencontre entre l’enzyme et son substrat, je recommande de baisser la probabilité de réaction, à 5% par tour (chaque tour, le complexe a une probabilité de 5% de se dissocier).
Dans la colonne de gauche (réactifs) on sélectionne complexe.
Dans la colonne de droite (produits) on sélectionne enzyme, galactose et glucose.
Il ne reste plus qu’à faire tourner le modèle en appuyant sur le bouton lecture (triangle pointant vers la droite) à gauche de l’écran.
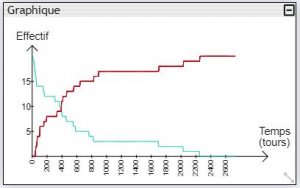
On voit alors le graphique se construire, les courbes obtenues ayant d’ailleurs à peu près l’allure de ce que l’on aurait obtenu in vitro.
Comment exploiter les données obtenues ?
A l’issue de l’exécution de notre modèle, nous obtenons un graphique. Ce graphique peut être exploité in situ, sans sortir du logiciel.
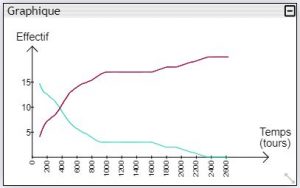
Il est tout d’abord possible de lisser le graphique ; cela estompera le caractère en « escalier » de la courbe (du au fait que les effectifs sont très modestes). L’algorithme utilisé étant celui de la « moyenne mobile », lisser la courbe aura pour effet d’en tronquer légèrement le début et la fin.
En survolant le graphique, les coordonnées (temps en tours, et effectif) correspondant à l’emplacement du pointeur de la souris sont données, permettant une lecture précise.
Il est aussi possible d’agrandir la fenêtre du graphique en tirant sur la poignée située en bas à droite de la fenêtre du graphique, ou encore de changer l’échelle horizontale à l’aide du curseur mobile.
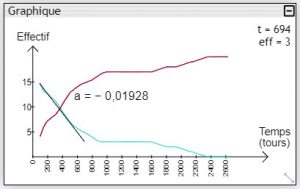
Si l’on souhaite faire de la cinétique, il est également possible de tracer une tangente et d’avoir sa pente (pour cela, il est recommandé de mettre l’exécution en pause au préalable). Il suffit de cliquer sur le graphique et de bouger la souris tout en maintenant le bouton enfoncé : un segment de droite apparaît alors, avec sa pente (coefficient directeur).
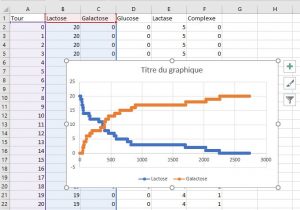
Enfin, il est possible d’exporter les données du graphique sous la forme d’un fichier CSV (fichier texte lisible par la plupart des tableurs, dont Excel et Openoffice), afin de l’exploiter dans un logiciel externe.
Quelle est l’intérêt pédagogique d’une telle approche ?
Les élèves sont sans cesse confrontés à des modèles dans leurs apprentissages, notamment en sciences. Cela peut s’avérer problématique, notamment lorsque les modèles sont utilisés comme des substituts de la réalité ; l’élève finit par croire que le modèle imite parfaitement le phénomène réel, ce qui est bien entendu impossible.
Proposer aux élèves non pas de « consommer » un modèle déjà réalisé mais de le créer (au moins partiellement) contribue à faire prendre conscience à l’élève de ce qui distingue un modèle de la réalité, d’en montrer les rouages en quelque sorte. C’est un peu comme si on invitait un élève fasciné par un spectacle de marionnettes, à passer derrière le rideau et à en tirer lui-même les ficelles ; beaucoup d’illusions tombent à ce moment là !
L’intérêt est donc réel, le délicat problème restant à résoudre est celui de la place précise d’une activité de modélisation (où l’élève crée un modèle) dans le scénario pédagogique.
Tout d’abord nous sommes convaincus qu’il n’est pas pertinent de partir un modèle pour construire un problème scientifique ; l’observation doit porter sur le réel (ou sur des documents le relatant) et non sur une abstraction virtuelle. Mettre les élèves face à un modèle comme s’il s’agissait de la réalité et leur faire réaliser des constats est un choix à notre avis difficile à défendre.
La modélisation peut par contre considérablement enrichir la compréhension que l’élève a du phénomène qu’il étudie. Cela peut se faire à différents niveaux.
Elle peut tout d’abord l’aider à construire son hypothèse. Le fait de demander à l’élève de construire le modèle à l’image de son hypothèse explicative revient à lui demander de faire l’effort de formaliser cette dernière. Si le modèle donne des résultats cohérents avec ceux observés, alors il est possible que l’explication formulée par l’élève soit elle-même cohérente. Attention, les résultats obtenus à partir d’un modèle (de ce niveau en tout cas) n’ont pas un statut de preuve. Seule la confrontation avec la réalité permet de valider définitivement une hypothèse: le modèle doit être éprouvé .
Elle peut ensuite accompagner l’élève dans son travail intellectuel de synthèse. L’activité de modélisation arrive alors en fin de séquence, quand toutes les réponses au problème scientifique ont été apportées. Elle peut alors se comparer (dans une certaine mesure) à la construction d’un schéma bilan, de synthèse ou fonctionnel, en rassemblant dans une construction unique toutes les entités, phénomènes et règles étudiées.
Liens :
Edu’modèles, module algorithmique
Sélection d’articles du site académique en rapport avec Edu’modèles