La dérive génétique est une notion qui reste abstraite pour beaucoup d’élèves, même si son étude s’appuie sur des exemples concrets. L’idée que le simple brassage aléatoire des allèles aboutisse inévitablement à une perte de biodiversité génétique reste contre-intuitive pour certains.
L’utilisation de modèles numériques ou analogiques (tirage de boules dans un chapeau) permet souvent de démontrer que le simple jeu du hasard aboutit bien à ce résultat prévisible. Cependant, les élèves, mais également les enseignants, font souvent remarquer que les modèles proposés ne prennent pas en compte la reproduction sexuée et la diploïdie des organismes.
Nous vous proposons un modèle qui, tout en restant très simple à comprendre, correspond de plus près à la réalité que les modèles usuels. Il n’est plus question d’un simple « tirage de boules », mais bien d’organismes diploïdes sexués, produisant des gamètes.
Présentation de l’interface :
(la fiche technique est téléchargeable ici, voir aussi à la fin de l’article)
Au lancement du logiciel, un premier écran invite l’utilisateur à saisir l’effectif, le nombre d’allèles ainsi que la probabilité d’éventuelles mutations.

Il est également possible de nommer les allèles, et de changer la couleur d’affichage de ceux-ci.
Enfin, il est possible de débrayer l’option qui assure qu’à chaque génération des mâles et des femelles seront présents (au risque de voir le modèle s’arrêter).
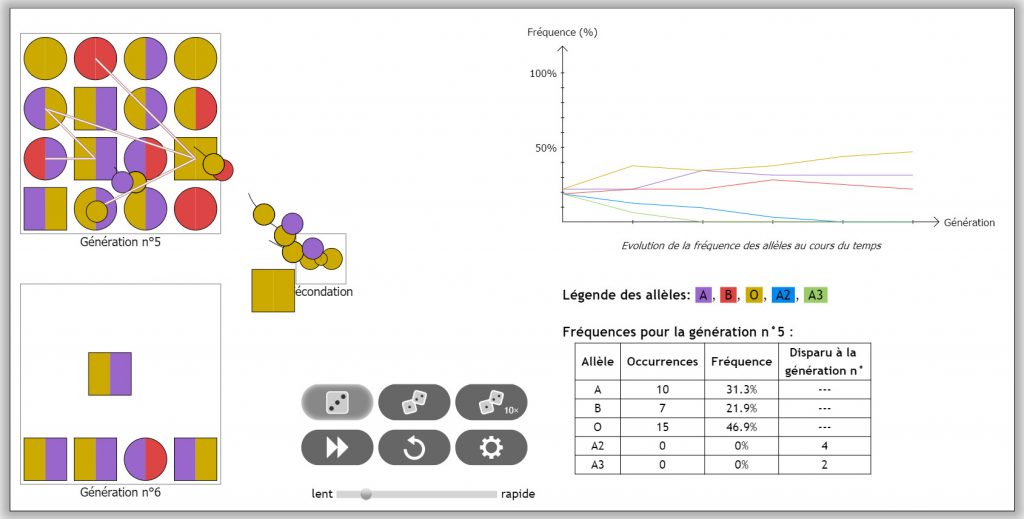
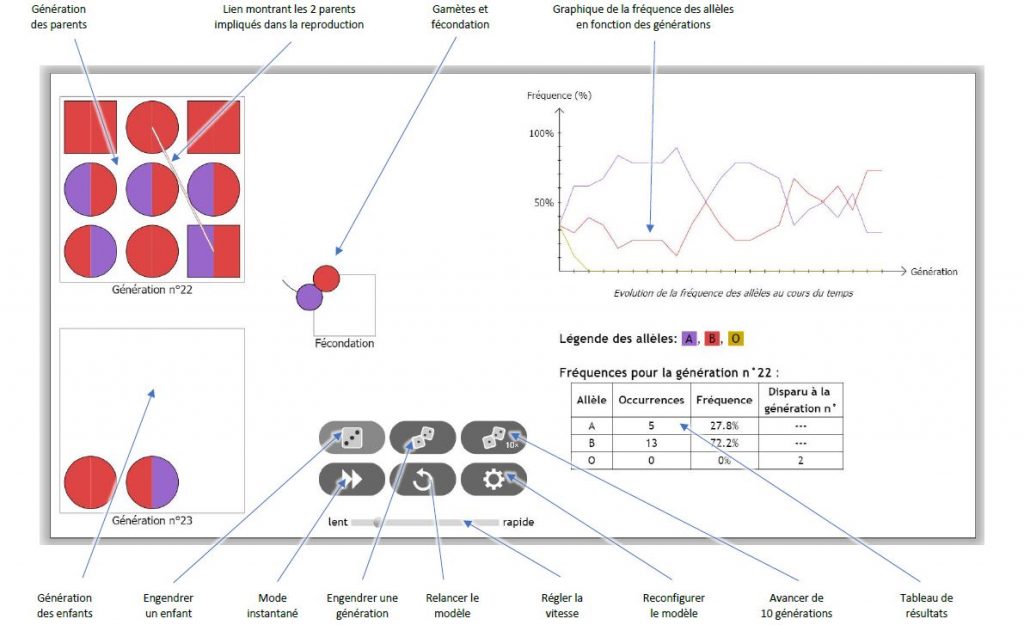
Lorsque l’utilisateur valide ces réglages, l’écran principal du modèle apparaît :
Sur cet écran, l’utilisateur peut engendrer les enfants par tirage, soit un par un, soit de manière groupée (une génération ou dix générations). Deux parents de sexes différents sont alors tirés au sort, les gamètes sont émis, la fécondation a lieu et l’enfant qui en est issu rejoint la génération suivante.
Il est possible de régler la vitesse, mais aussi d’enclencher un « mode instantané » qui permettra d’avancer très vite dans les générations.
Un graphique permet de suivre l’évolution temporelle de la fréquence des allèles, ainsi qu’un tableau récapitulatif qui indique à quelle génération un allèle a disparu.
Pistes d’exploitation :
Un modèle est une représentation simplifiée de la réalité, s’appuyant sur des hypothèses, des règles etc. Ainsi, il nous semble inapproprié d’utiliser un modèle comme point de départ d’un apprentissage. Il sera par contre très utile pour vérifier si les explications (ou les hypothèses) proposées par l’élève peuvent bien rendre compte du phénomène observé.
La démarche que nous proposons est la suivante :
situation déclenchante où la diversité génétique a diminué au cours du temps, dans une population d’effectif réduit (ex. lions du Ngorongoro)
⇓
émergence d’un problème
« Comment expliquer cette baisse de biodiversité génétique ? »
⇓
formulation d’une hypothèse
« On suppose que l’effectif réduit de la population est responsable de la disparition de certains allèles »
⇓
utilisation du modèle et exploitation statistique des résultats pour vérifier cette hypothèse (voir paragraphe plus bas)
⇓
validation de l’hypothèse (la baisse de diversité est d’autant plus rapide que l’effectif est faible)
⇓
proposition d’un mécanisme :
« Les brassages aléatoires associés à la reproduction sexuée sont à l’origine de la disparition de certains allèles dans la population »
⇓
formulation d’une conclusion
Exploitation statistique du modèle :
Il n’est pas indispensable d’aller jusqu’à une collecte, une mutualisation voire une exploitation statistique des résultats issus du modèle. Mais cela reste un exercice intéressant d’un point de vue méthodologique, qui sensibilisera l’élève à la nécessité de réaliser un grand nombre de relevés pour que ceux-ci soient significatifs.
L’idée est de déterminer le nombre moyen de générations nécessaire pour qu’il ne reste plus qu’un seul allèle en fonction de l’effectif de la population.
Vu le nombre important d’essais (et donc de tirages !), il est impensable qu’un seul élève ou binôme réalise l’intégralité des relevés. Cela incitera les élèves à mutualiser les résultats, à l’aide d’une feuille de calcul partagée par exemple.
Deux organisations (au moins) sont alors envisageables :
– chaque élève (ou binôme selon le nombre d’élèves par poste) réalise plusieurs essais pour un effectif donné, relève pour chaque essai le nombre de générations au bout duquel tous les allèles (sauf un) ont disparu, puis réalise une moyenne à partir de ces nombres
– chaque élève réalise un essai pour chaque effectif, et relève à chaque fois le nombre de générations au bout duquel tous les allèles (sauf un) ont disparu
Au terme de ces tirages, les résultats sont mutualisés dans un tableau qui pourrait ressembler à ceci :
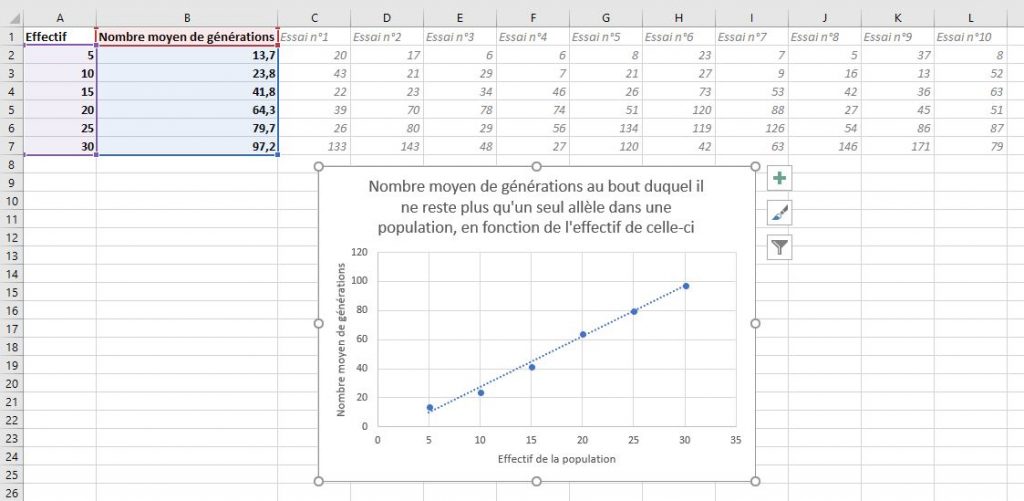
Le graphique obtenu montre qu’il existe bien une relation (linéaire ?) entre l’effectif d’une population et le nombre de générations au bout duquel il ne reste qu’un seul allèle pour un gène donné.
Les élèves sont souvent surpris (et c’est une bonne chose) des écarts immenses entre les relevés pour un effectif donné. Il n’a fallu que 27 générations pour une population de 30 individus, alors que 52 générations ont été nécessaires pour une population de 10 individus. Cela contribue à leur faire réaliser que des écarts individuels peuvent aller à l’encontre d’une tendance statistique (une fille peut présenter une taille supérieure à un garçon).
Conclusion :
S’il ne doit pas se substituer à la réalité, un modèle numérique comme celui-ci peut s’avérer très utile pour facilité la compréhension de notions abstraites telles que la dérive génétique.
Grâce à ce modèle, l’élève pourra mettre à l’épreuve l’hypothèse qu’il aura émis pour expliquer la baisse de diversité génétique observée (sur documents par exemple), mais également proposer un mécanisme qui ne pourra être pleinement appréhendé qu’en regardant le logiciel fonctionner.
Liens :
– application « en ligne » :
https://www.pedagogie.ac-nice.fr/svt/productions/derive-diplo/index.htm
– application « hors-ligne » :
https://www.pedagogie.ac-nice.fr/svt/productions/derive-diplo/derive-diplo-local.zip
– fiche technique :
https://www.pedagogie.ac-nice.fr/svt/productions/derive-diplo/FT-derive-diplo.pdf
Auteur : Philippe Cosentino