par Julien Cartier, professeur de SVT au lycée Carnot de Cannes
Avant-propos
Cette série d’articles vise à fournir aux professeurs de SVT intervenant en enseignement scientifique de première des ressources utiles pour bâtir leur cours sur la datation scientifique de la Terre. Or, s’agissant d’histoire des sciences il importe de se méfier par-dessus tout des caricatures qui abondent, hélas, dans la littérature de vulgarisation comme sur internet. Ainsi, contrairement à ce qu’on lit un peu partout Ussher fut bien davantage un historien qu’un théologien, Buffon n’a pas escamoté ses datations par peur de l’Inquisition et Darwin n’a jamais daté le globe terrestre. Les raccourcis et les idées reçues brossent un tableau mensonger de la Science où quelques génies en lutte contre l’obscurantisme parviennent, seuls, à faire progresser l’entendement humain vers des vérités indépassables. Pour y remédier il importe de revenir aux sources, c’est-à-dire aux écrits de tous ces savants dont la pensée et les travaux ont alimenté le questionnement scientifique vis-à-vis de l’âge de notre planète. Au lieu de se moquer de leurs erreurs il convient de souligner leur nature féconde. Plutôt que de considérer que ceux qui autrefois ont pensé autre chose que ce que l’on pense aujourd’hui ont forcément mal pensé, il faut garder à l’esprit que penser faux ce n’est pas nécessairement mal penser. Buffon, Cuvier ou encore Kelvin, pour ne prendre que ces trois exemples, étaient tout sauf des idiots ou de mauvais scientifiques. Mais la cohérence de leurs théories n’apparaît qu’à la condition de s’intéresser aux savoirs de leurs époques respectives. À défaut, nos condamnations se réduisent souvent à des jugements anachroniques.
Voilà pourquoi on trouvera dans ces articles de très nombreux extraits des ouvrages de ces savants, pour la plupart disponibles en ligne sur le site de la BnF, Gallica, ou dans la bibliothèque numérique Google Books. Deux types de lecture sont possibles : soit le texte et les citations, soit pour le lecteur pressé le texte seul. L’ensemble des articles forme un tout cohérent, mais sa longueur m’a incité à le subdiviser en plusieurs parties afin d’en faciliter la lecture par un collègue désireux d’y puiser rapidement des ressources pédagogiques.
Concernant la bibliographie contemporaine, il me semble que l’enseignant se trouve surtout confronté à la difficulté de choisir parmi l’abondance de titres à sa disposition. Aussi me paraît-il opportun de limiter la bibliographie correspondante aux quelques titres suivants, tous remarquables et d’une lecture aisée :
- Stephen Jay Gould, Aux racines du temps, 1987
- François Ellenberger, Histoire de la géologie, 1988 (tome 1), 1994 (tome 2)
- Pascal Richet, L’âge du monde, 1999
- Vincent Deparis et Hilaire Legros, Voyage à l’intérieur de la Terre, 2000
- Gabriel Gohau, Les sciences de la Terre au XVIIe et XVIIIe siècles, naissance de la géologie, 1990
- Gabriel Gohau, Naissance de la géologie historique, 2003
On trouvera une bibliographie plus détaillée à la fin du dernier article.
Remerciements
Je tiens à remercier chaleureusement François Besset, professeur de philosophie, ami précieux et grand spécialiste d’Aristote, lequel a bien voulu m’expliquer la pensée de ce savant et se plier au fastidieux exercice consistant à traduire les propos ésotériques de Kepler.
Je remercie également Patrick Tort de m’avoir orienté vers son collègue Guido Chiesura qui m’a fort aimablement communiqué des extraits de l’ouvrage que Sandra Herbert a consacré au travail géologique de Darwin. Mme. Herbert elle-même a très gentiment répondu à mes questions et m’a permis de comprendre comment Darwin était parvenu à calculer l’âge de la vallée de Weald. Je lui en sais gré.
Enfin, j’exprime la plus sincère gratitude à Jeanne Passoni dont la patiente relecture de mes manuscrits permet d’en expurger les fautes d’orthographe qui s’y forment aussi sûrement que le plomb radiogénique dans les météorites.
Ce travail est dédié à mon regretté professeur Jean-Marc Drouin, dont les cours au Muséum National d’Histoire Naturelle et les livres inestimables, m’ont donné le goût de l’histoire et de l’épistémologie des sciences.
ARTICLE 4/4 : l’empire de lord Kelvin et le poids des atomes
ARTICLE 1/4 : de l’éternité aux mondes éphémères
ARTICLE 2/4 : les chronomètres naturels, de Halley à Buffon
ARTICLE 3/4 : la Terre sans âge, de Lyell à Darwin
De Buffon à Kelvin
Rétrospectivement le travail de Buffon souffre d’un biais majeur : il suppose que la température de la Terre est uniforme. Souvenons-nous qu’il arrête le chronomètre lorsque la température du boulet devient égale à la température ambiante. Buffon imagine donc que dans un passé relativement récent la surface terrestre était plus chaude qu’aujourd’hui, alors que nous considérons que la température de surface a relativement peu varié depuis des centaines de millions d’années (les variations climatiques mises à part). En réalité, Buffon mesure la température de la surface du boulet, pas sa température interne.
On l’a dit Kelvin ne partage pas la conception de Lyell d’une Terre éternellement chaude. Il pense au contraire que la planète se refroidit peu à peu. Mais, contrairement à Buffon, Kelvin sait que le refroidissement d’un objet ne se réalise pas de manière uniforme. Pour le comprendre il n’y a rien de mieux qu’une dinde sortant du four. A cet instant, notre dinde présente une température uniforme de 200°C. Puis, elle commence à se refroidir.
Mais, poursuivons notre comparaison. La dinde ne se refroidit pas de façon homogène :
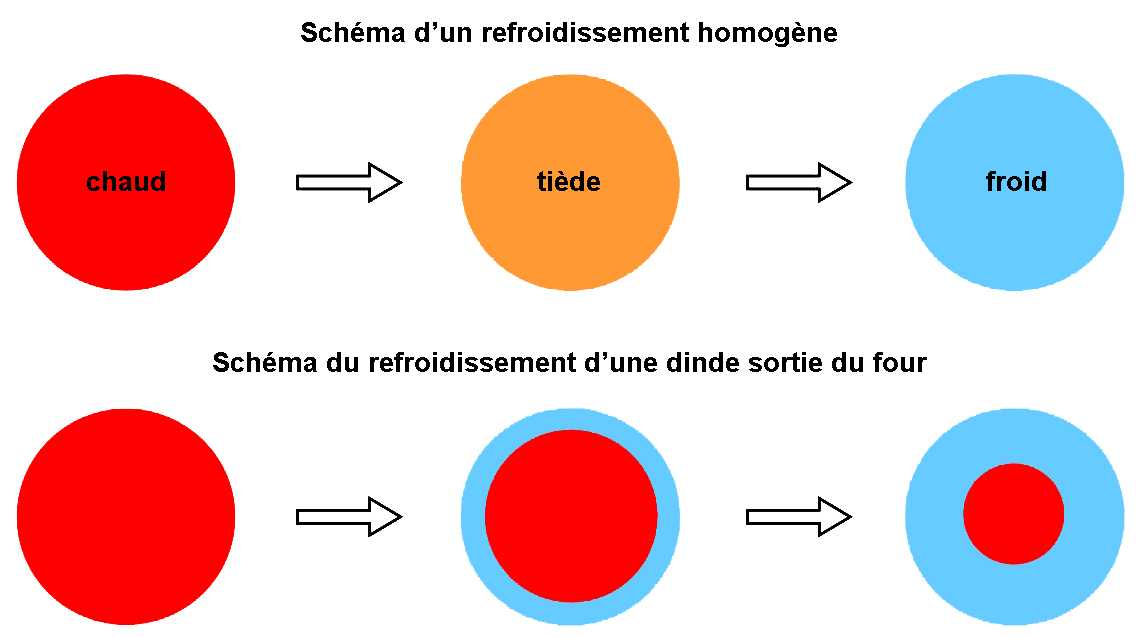
C’est d’abord la surface de la dinde qui se refroidit tandis que l’intérieur reste brûlant. Les cuisiniers le savent : le cœur de la dinde continue de cuire après être sortie du four et il faut se méfier de cette cuisson à l’air libre capable de gâcher le plat.
Comparons avec la variation de la température à l’intérieur de la Terre. Attention, on a tendance à « lire » cette image de haut en bas et de gauche à droite, alors que le sens de lecture le plus pertinent est exactement inverse :
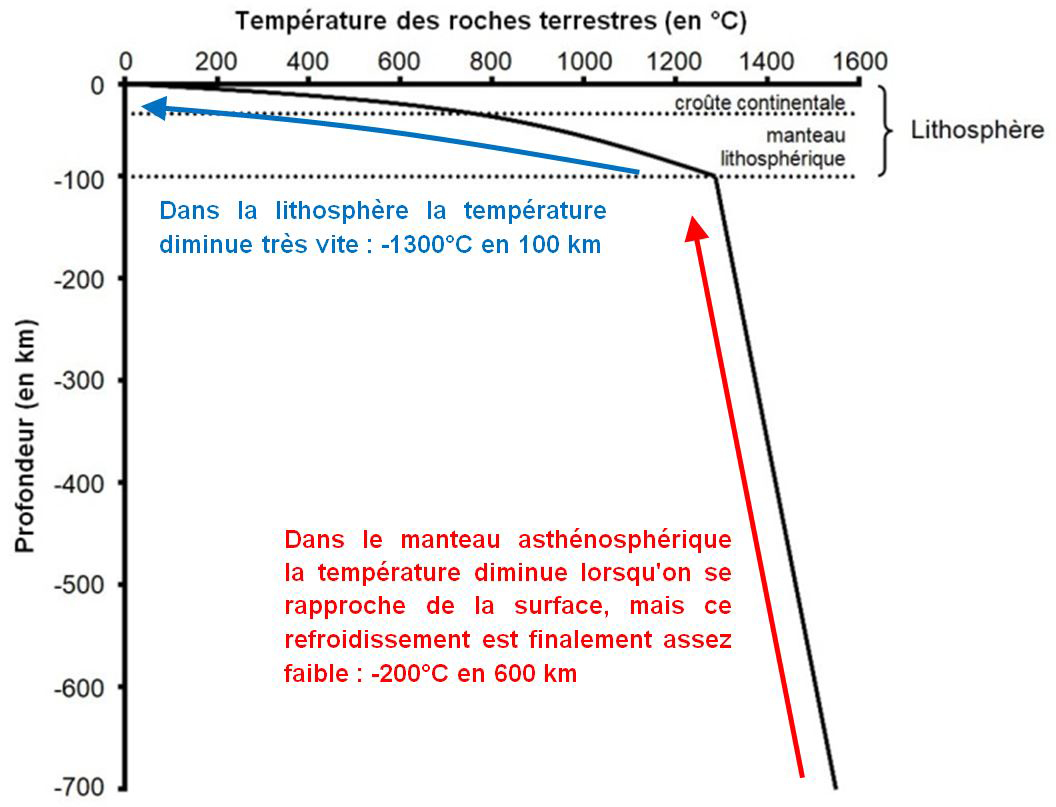
On peut donc légitimement comparer la Terre a une dinde en train de se refroidir : l’intérieur est encore très chaud, tandis que la couche froide en surface correspond à la lithosphère, ce que les géologues appellent une « couche limite thermique ». Plus la Terre est ancienne, plus elle s’est refroidie, et plus elle s’est refroidie plus sa lithosphère est épaisse. Voilà le raisonnement que va utiliser Kelvin.
Cette brillante idée il la doit à la lecture du travail d’un mathématicien et physicien français, Joseph Fourier. En 1822 il publie les résultats des recherches qu’il mène depuis plus de 10 ans sur la diffusion de la chaleur :
- Joseph Fourier, Théorie analytique de la chaleur, 1822
Les effets de la chaleur sont assujettis à des lois constantes que l’on ne peut découvrir sans le secours de l’analyse mathématique. La Théorie que nous allons exposer a pour objet de démontrer ces lois ; elle réduit toutes les recherches physiques, sur la propagation de la chaleur, à des questions de calcul intégral dont les éléments sont donnés par l’expérience. Aucun sujet n’a des rapports plus étendus avec les progrès de l’industrie et ceux des sciences naturelles ; car l’action de la chaleur est toujours présente, elle pénètre tous les corps et les espaces, elle influe sur les procédés des arts, et concourt à tous les phénomènes de l’univers. Lorsque la chaleur est inégalement distribuée entre les différents points d’une masse solide, elle tend à se mettre en équilibre, et passe lentement des parties plus échauffées dans celles qui le sont moins ; en même temps elle se dissipe par la surface, et se perd dans le milieu ou dans le vide. Cette tendance à une distribution uniforme, et cette émission spontanée qui s’opère à la surface des corps, changent continuellement la température des différents points. La question de la propagation de la chaleur consiste à déterminer quelle est la température de chaque point d’un corps à un instant donné, en supposant que les températures initiales sont connues (…) Si l’on place une masse solide homogène, de formé sphérique ou cubique, dans un milieu entretenu à une température constante, et qu’elle y demeure très longtemps plongée, elle acquerra dans tous ses points une température très peu différente de celle du fluide. Supposons qu’on l’en retire pour la transporter dans un milieu plus froid, la chaleur commencera à se dissiper par la surface ; les températures des différents points de la masse ne seront plus sensiblement les mêmes, et si on la suppose divisée en une infinité de couches par des surfaces parallèles à la surface extérieure, chacune de ces couches transmettra, dans un instant, une certaine quantité de chaleur à celle qui l’enveloppe (…) On considérera ensuite que, pendant la durée du refroidissement, il s’écoule à chaque instant, par la surface extérieure, une certaine quantité de chaleur qui passe dans le milieu. La valeur de cette quantité n’est pas constante ; elle est plus grande au commencement du refroidissement (p.2-6).
De 1841 à 1843, Kelvin écrit plusieurs articles sur les lois de Fourier, et dans les années qui suivent il envisage la possibilité de dater la Terre à l’aide des données géothermiques (De Motu Caloris per Terrae Corpus, 1841 ; On the distribution of the heat through the body of the earth, 1846). Mais, à l’époque le gradient géothermique était encore trop mal connu pour mener à bien cette datation.
Ce problème a été résolu lorsqu’en 1861 il décide de se repencher sur la question. On estime alors le gradient géothermique aux alentours de 36°C/km, un ordre de grandeur tout à fait acceptable. Encore faut-il savoir qu’au XIXème siècle on pense que la température originelle de la Terre était très précisément de 3900°C, car c’est la température que l’on prête alors – à tort – aux roches en fusion. A raison de 36°C/km, cette température maximale doit donc être atteinte à moins de 100 km de profondeur (80,5 km précisément).
Kelvin est néanmoins contraint d’émettre deux hypothèses : tout d’abord que la Terre soit entièrement solide et relativement homogène dans sa composition (ce qui exclu une structure en couches concentriques de nature différentes), ensuite que le refroidissement se fait uniquement par conduction (pas de convection donc).
Normalement, la loi de Fourier appliquée à une sphère considère la diffusion de la chaleur dans les 3 dimensions (x, y, z). Mais, comme la couche froide à la surface de la Terre où la température varie est très mince, Kelvin estime que l’on peut se limiter à une seule dimension (z). Ce qui nous donne l’équation suivante :
dT/dz = T0 / (t . k. π)
dT/dz = variation de la température en fonction de la profondeur = gradient géothermique = 36°C / km
T0 = 3900°C
t = temps
k = constante de diffusion des roches, déterminée en laboratoire par Kelvin à 1,2.10-6 m2/s
Le 1er janvier 1862, Kelvin présente ses résultats dans un article intitulé « On the secular cooling of the Earth » (Sur le refroidissement séculaire de la Terre) publié dans la revue scientifique Transactions of the Royal Society of Edinburgh. Et il commence par une attaque implicitement adressée à Lyell :
Depuis dix-huit ans, j’ai insisté sur le fait que les principes essentiels de la thermodynamique ont été négligés par les géologues qui, sans compromis, s’opposent à toutes les hypothèses catastrophistes, et soutiennent que (…) les phénomènes n’ont jamais été plus violents dans le passé qu’ils ne le sont actuellement. Il est tout à fait certain que le système solaire n’a pas pu fonctionner, comme il le fait actuellement, pendant plusieurs centaines de milliers ou de millions d’années, sans perte irrévocable (par dissipation) d’une proportion considérable de toute l’énergie initialement en réserve dans la chaleur du soleil et dans la chaleur de la Terre (plutonique) (…) Le fait que la température augmente avec la profondeur implique une perte de chaleur par conduction, de l’intérieur vers l’extérieur à travers la croûte supérieure. Par conséquent, puisque la croûte supérieure ne devient pas plus chaude d’année en année, il doit exister une perte séculaire de chaleur de toute la Terre (…) Il est certain que soit la Terre devient dans l’ensemble plus froide au cours du temps, soit la chaleur est générée à l’intérieur par une réaction chimique. Il faut alors supposer, comme l’a fait Lyell, que les substances, combinées entre elles, peuvent être à nouveau séparées par électrolyse, sous l’effet de la chaleur libérée par leur combinaison, de sorte que ce phénomène chimique continuerait dans un cycle sans fin, violant les principes de la philosophie naturelle, exactement de la même façon que le ferait une horloge qui se remonterait automatiquement afin de fonctionner éternellement pour répondre aux attentes de son ingénieux inventeur.
Kelvin propose alors une fourchette de datations allant de 98 à 200 millions d’années :
Pour les géologues qui ont besoin des périodes les plus longues, la meilleure option correspond à la théorie de Leibniz qui suppose simplement que la Terre a été à un moment entièrement à l’état de liquide incandescent, sans expliquer comment elle serait entrée dans cet état. Si nous supposons que la température de la roche en fusion était d’environ 10 000°F (5538°C), une estimation très haute, la consolidation peut avoir eu lieu il y a 200 millions d’années. Mais, si nous supposons que la température de la roche en fusion était de 7000°F (3871°C), ce qui correspond à l’estimation la plus courante, on peut supposer que la consolidation a eu lieu il y a 98 millions d’années. Ces estimations sont fondées sur la solution de Fourier.
Prudent, il précise que l’on doit élargir cette fourchette entre 20 et 400 millions d’années :
Mais nous sommes très ignorant des effets des températures élevées sur la modification des conductivités, des chaleurs spécifiques des roches, et de leur chaleur latente de fusion. Nous devons donc admettre des limites très larges dans l’estimation que j’ai tenté de réaliser. Cependant, je pense que nous pouvons dire avec une grande probabilité que la consolidation ne peut avoir eu lieu il y a moins de 20 millions d’années, sans quoi nous observerions une chaleur souterraine supérieure à celle que nous mesurons actuellement, ni il y a plus de 400 millions d’années.
L’article s’achève sur le rappel que son travail suppose une Terre majoritairement solide, afin d’écarter les transferts de chaleur par convection :
J’ai récemment démontré, concernant l’état actuel de la Terre intérieur, qu’il n’est pas, comme on le suppose communément, entièrement liquide sous une mince croûte de 30 à 100 miles d’épaisseur, mais que la Terre est dans l’ensemble plus rigide qu’un globe solide continu de verre du même diamètre, et probablement qu’un en acier.
La datation de Kelvin s’accordait plutôt bien avec celle de Phillips (98 millions d’années pour l’ensemble de la colonne stratigraphique), lequel est d’ailleurs cité dans l’article précédent comme l’un des géologues à l’origine de la détermination du gradient géothermique. Mais, l’entente sera de courte durée. Car quelques mois plus tard Kelvin publie un nouvel article dans la revue Macmillan’s Magazine, intitulé « On the Age of the Sun’s Heat » (L’âge de la chaleur du Soleil). A cette époque deux hypothèses s’affrontent à propos de l’origine de l’énergie solaire. Certains imaginent que notre étoile est continuellement alimentée par une pluie de poussières et d’astéroïdes qui lui servent de combustibles. D’autres défendent que le Soleil s’est formé par accrétion de poussières et d’astéroïdes dont l’énergie cinétique a été convertie en chaleur. Kelvin était progressivement devenu un partisan de la seconde hypothèse. Dans cet article, il tente d’estimer l’âge du Soleil en fonction de la vitesse de sa contraction gravitationnelle. Les données précises font largement défaut aussi est-il contraint de spéculer sur la densité des différentes parties de l’étoile ou encore sur la chaleur qu’elle rayonne (loin de la précision des calculs du travail sur l’âge de la Terre, on croirait revoir les estimations au doigt mouillé de Darwin). Cela ne l’empêche pas de proposer une fourchette d’âges théoriques :
Cela prolongerait trop cet article et exigerait de nombreux développements mathématiques pour expliquer pleinement les principes sur lesquels se fonde cette dernière estimation. Il suffit de dire que des corps, tous beaucoup plus petits que le soleil, tombant ensemble d’un état de repos relatif (…) et formant un globe de densité uniforme égale en masse et en diamètre au soleil, générerait une quantité de chaleur qui, calculée avec précision selon les principes de Joule et les résultats expérimentaux, ne serait que 20 000 000 fois l’estimation de Pouillet de la quantité annuelle de rayonnement solaire. Cependant, la densité du soleil doit, selon toute probabilité, augmenter beaucoup vers son centre, et donc celui-ci doit libérer une quantité de chaleur considérablement plus grande que celle qui doit être supposée si sa densité était homogène. De plus, on ne sait pas quelle quantité de chaleur a pu être dissipée par la résistance et les chocs mineurs avant l’agglomération finale (…) Il semble donc, dans l’ensemble, très probable que le soleil n’ait pas illuminé la Terre depuis plus de 100 millions d’années, et presque certain qu’il ne l’a pas fait depuis plus de 500 millions d’années.
Le Soleil aurait donc entre 20 et 500 millions d’années. Et Kelvin en profite pour régler son compte à l’estimation de Darwin :
Que devons-nous penser des estimations géologiques donnant 300 millions d’années pour la dénudation du Weald ? Est-il plus probable que les conditions physiques de la matière solaire diffèrent 1 000 fois de ce que la thermodynamique nous oblige à supposer; ou qu’une mer agitée, avec peut-être des marées de la Manche d’une extrême violence, devrait empiéter sur une falaise de craie 1 000 fois plus rapidement que l’estimation de M. Darwin d’un pouce par siècle ?
En réalité, les critiques de Kelvin vont devenir de plus en plus virulentes. Voici par exemple la première phrase du discours qu’il prononce le 27 février 1868 devant la Société Géologique de Glasgow (il sera publié la même année sous le titre On Geological time) : « une GRANDE réforme de la spéculation géologique semble être devenue nécessaire ».
Kelvin concentre ses attaques sur John Playfair, un géologue qui popularisa les travaux de James Hutton considéré comme le père de l’uniformitarisme. C’est un moyen d’attaquer indirectement Charles Lyell, relativement protégé par sa notoriété et son prestige. L’article de Kelvin lui offre une nouvelle fois l’occasion d’affirmer que la Terre doit être bien moins vieille que ne le prétendent certains géologues. Il ne cache pas que le calcul de son âge est rendu compliqué par la difficulté que rencontrent les scientifiques à mesurer précisément le gradient géothermique. Néanmoins, s’appuyant une nouvelle fois sur son estimation de l’âge du Soleil, il termine en affirmant que le globe terrestre ne doit pas avoir plus de 100 millions d’années.
C’est Thomas Henry Huxley, le célèbre ami de Darwin, qui répondit à Kelvin dans un article publié en 1869 et intitulé On geological reform :
Les mathématiques peuvent être comparées à un moulin… ce que vous en retirez dépend de ce que vous y mettez ; et comme le meilleur moulin du monde n’extraira jamais de la farine de blé à partir de graines de pois, les pages de formules n’obtiendront jamais un résultat définitif à partir de données imprécises.
Cela résume assez bien le point de vue d’un grand nombre de géologues à cette époque, lequel pourrait s’énoncer ainsi : les calculs des physiciens sont peut-être impressionnants mais leurs résultats ne sont pas fiables parce qu’ils reposent sur des données discutables. Et nous connaissons bien l’imperfection de ces chiffres puisqu’ils proviennent des études que nous réalisons sur le terrain.
Mais, tous les géologues ne partagent pas cette opinion et certains vont même s’efforcer de produire des datations compatibles avec celles de Kelvin, par exemple en réévaluant les vitesses d’érosion et de sédimentation. Outre John Phillips, c’est par exemple le cas du spécialiste de l’érosion fluviale Archibald Geikie.
Parmi les méthodes originales datant de cette fin du XIXème siècle on peut citer celle de Georges Howard Darwin, le cinquième enfant de Charles, physicien très proche de Kelvin, qui en 1879, dans un article intitulé On the precession of a viscous spheroid, and on the remote history of the Earth, se fonde sur la vitesse à laquelle la Lune s’éloigne de la Terre pour calculer que les deux astres devaient être réunis il y a seulement 54 millions d’années (en vérité il s’agit de l’estimation la plus basse). On connaît également le travail du physicien et géologue John Joly qui en 1899, redécouvrant le chronomètre imaginait par Halley presque deux siècles plus tôt, essaye de déterminer le temps nécessaire pour que l’apport en sel des rivières conduise à la salinité actuelle des océans. Joly ne se base que sur le taux de sodium. Connaissant sa teneur moyenne dans l’eau de mer, il estime la quantité totale de sodium dans les océans à 15,627.1015 tonnes et les apports continentaux à 27 180 km3 d’eau de rivière à raison de 5,787g de sodium par m3. Il trouve ainsi 99 millions d’années, qu’il ramène à un intervalle compris entre 80 et 89 millions en tenant compte de quelques facteurs secondaires (ce travail est publié dans un article intitulé An estimate of the geological age of the Earth). Bien sûr le calcul de Joly est faux puisqu’il ignore que les roches du plancher océanique fixent le sel. Mais, pour sa décharge, il faut se souvenir qu’à cette époque personne ne sait que le fond des mers est composé de basaltes. En revanche, sa proposition s’accordait déjà fort mal avec le fait que les roches sédimentaires marines les plus vieilles semblaient tout aussi riches en sel que les récentes et qu’elles renfermaient des organismes fossilisés dont les formes étaient semblables aux espèces actuelles adaptées à la vie en eau salée.
Le divorce va encore s’accentuer lorsqu’en 1893, Clarence King, un géologue américain, parvient à la conclusion que la température maximale des roches terrestres ne doit pas excéder 2000°C et non 3900°C comme Kelvin le supposait initialement. Il rédige alors un article (The age of the earth) aboutissant à un âge d’à peine 24 millions d’années pour aboutir au gradient géothermique actuel. C’est cette nouvelle estimation que Kelvin défendra sur la fin de sa vie, s’attirant non seulement l’hostilité des géologues, y compris de vieux partisans comme Geikie, mais aussi des biologistes qui ne voient pas comment concilier leur révolution évolutionniste avec une chronologie aussi courte.
Le dernier chronomètre
On croit généralement que l’erreur de Kelvin s’explique par l’absence de prise en compte de la chaleur produite par la radioactivité, laquelle radioactivité ne fut découverte qu’en 1896 et sa capacité à libérer une grande quantité de chaleur en 1903. C’est parfaitement exact en ce qui concerne l’âge du Soleil. Mais, cette correction ne changerait pratiquement rien à son calcul de l’âge de la Terre. En effet, Kelvin considère que depuis la formation de la Terre seule la chaleur contenue dans les 80 premiers kilomètres de profondeur a pu diffuser jusqu’à la surface. S’il avait connu la radioactivité il aurait donc modifié son raisonnement afin de prendre en compte la quantité de chaleur d’origine radioactive issue de ces seuls 80 kilomètres. Or, autant la quantité de chaleur émise par la désintégration des éléments radioactifs répartis dans l’ensemble du volume de la Terre est tout à fait considérable, autant la quantité de cette chaleur formée dans le seul volume de la lithosphère est relativement négligeable dans le calcul de Kelvin.
En réalité, l’erreur de Kelvin réside essentiellement dans sa certitude que le globe est parfaitement solide, condition sine qua non pour y appliquer strictement les lois de Fourier. Pas question donc d’envisager que l’intérieur de la planète puisse être animé de mouvements de convection. La conviction de Kelvin repose sur son étude des marées qui indique indéniablement que les 1500 premiers kilomètres du globe, au moins, doit être aussi rigides que de l’acier. Ce faisant il néglige les observations des géologues qui, à partir du phénomène d’isostasie et des déformations plastiques des roches (les plis), admettent la possibilité que les matériaux terrestres se comportent comme des fluides. Curieusement, c’est l’un de ses anciens étudiants, John Perry, qui tente, en vain, d’attirer l’attention du vieil homme sur la possibilité qu’une convection interne rallonge considérablement l’âge de la Terre. Il convient de noter que l’hypothèse d’une convection des matériaux terrestres a été formulée par Osmond Fisher dans un livre paru en 1881 : Physics of the Earth’s Crust. Perry se contente donc de tirer les conséquences logiques de ce phénomène sur le refroidissement des couches superficielles du globe.
Pour comprendre le rôle de la convection sur l’estimation de l’âge de la Terre à partir de son gradient géothermique il faut revenir à notre métaphore de la dinde sortant du four. Bien évidemment, l’intérieur de cette dinde ne subit aucune convection. Mais, imaginons qu’au lieu de la farce il s’y trouve un liquide brûlant. Celui-ci serait animé de mouvements de convections qui amèneraient en permanence du liquide chaud au contact de la couche froide située en surface. Cela ralentirait considérablement le refroidissement de cette couche, dont l’épaisseur croîtrait beaucoup plus lentement que si la chaleur de la dinde n’était évacuée que par conduction.
En 1895, John Perry s’adresse donc à Kelvin par l’intermédiaire de la revue Nature, créée en 1869 et qui jouit déjà d’un écho particulier au sein de la communauté scientifique. Dans son article, intitulé On the age of the earth, Perry montre qu’en admettant l’existence de mouvements convectifs l’âge de la Terre peut être réévalué à plusieurs milliards d’années. Kelvin lui répond poliment dans la même revue et, étonnamment, semble envisager la possibilité qu’il se soit trompé :
Je pensais que mon intervalle de temps de 20 à 400 millions d’années était assez large, mais il est tout à fait possible que j’eusse dû placer la limite supérieure beaucoup plus haut, à 4000 peut-être au lieu de 400 millions d’années.
Mais, si Kelvin accepte de reconsidérer sa datation du globe terrestre, il n’en va pas de même pour celle du Soleil. En effet, il lui semble désormais certain que l’énergie de cette étoile ne provient pas d’une alimentation en poussières et autres astéroïdes. Dès lors, la fission et la fusion nucléaire étant encore inconnues, il ne lui reste comme source de chaleur que la contraction gravitationnelle. Et, sur ce point, ses calculs sont formels : le Soleil ne peut être aussi vieux.
Survient alors, une révolution inattendue. En 1896, Henri Becquerel découvre la radioactivité. Sept ans plus tard Pierre Curie et Albert Laborde parviennent à mesurer la chaleur émise par la désintégration du radium (découvert en 1897 par Marie Curie). Et cette chaleur dépasse de beaucoup tout ce que les physiciens avaient imaginé. La nouvelle fait grand bruit et pousse Robert Strutt, le fil de lord Rayleigh, à étudier la teneur en radium des roches et des minéraux terrestres. C’est lui qui va découvrir qu’il y a dix fois plus de radium dans la croûte continentale que dans la croûte océanique. Surtout, il montre, dès 1905, que la quantité de radium dans la croûte est si élevée qu’il est impossible d’imaginer la même concentration dans les roches du manteau et du noyau, sans quoi la Terre se réchaufferait au lieu de se refroidir. Il faut donc supposer que la majeure partie des éléments radioactifs se concentrent dans la croûte. Soudainement, le refroidissement de la Terre ne constitue plus une limite à l’extension de son âge. Elle dispose en réalité d’une immense source de chaleur interne.
Paradoxalement, la chaleur d’origine radioactive rend pratiquement caduque l’utilisation de la vitesse du refroidissement planétaire comme chronomètre naturel, car on ignore alors trop de choses sur la radioactivité (teneur exacte des éléments aux différentes profondeurs, diversité des radioéléments, quantité de chaleur libérée au cours du temps, etc.). Sans compter que la convection mantellique qui compte de plus en plus de partisans, reste trop méconnue pour pouvoir quantifier son influence sur ce refroidissement.
Il faut donc trouver un nouveau chronomètre naturel. Et ce sont deux jeunes chimistes, futurs prix Nobel, qui vont l’imaginer : Ernest Rutherford et Frededick Soddy. En 1902, ils comprennent que la désintégration d’un élément radioactif correspond en réalité en sa transmutation en un autre élément. Rutherford en déduit une méthode de datation : puisque la désintégration du radium donne naissance à de l’hélium, il suffit de mesurer la concentration de ce dernier dans les minéraux pour accéder à leur âge. Dès 1904, le premier échantillon analysé affiche 40 millions d’années et l’année suivante Rutherford annonce 140 millions d’années, soit déjà plus que l’estimation haute de Kelvin. Bien sûr, les incertitudes sont nombreuses, à commencer par la présence d’hélium non radiogénique et l’imperfection des méthodes de mesures. Ainsi, c’est le même minéral qui entre 1904 et 1906 affiche 40, puis 140 et enfin 400 millions d’années, déroutant quel que peu le malheureux Rutherford !
Lord Kelvin meurt en 1907. Cela lui laisse le temps d’assister à cet immense chamboulement. On se souvient par exemple qu’en 1904 il assiste à une conférence de Rutherford, lequel raconte comment il parvint à éviter de froisser le vénérable savant :
J’entrai dans la pièce, qui était plongée dans une semi-obscurité, et remarquai bientôt lord Kelvin dans l’assistance ; je me rendis compte que j’allais avoir quelques difficultés avec la dernière partie de mon intervention concernant l’âge de la Terre, où mes vues étaient en contradiction avec les siennes. À mon grand soulagement, il s’endormit profondément, mais au moment où j’abordais le point important, je vis le vieil oiseau se redresser sur son siège, ouvrir un œil et me lancer un regard torve ! Une inspiration me vint alors, et je déclarai que lord Kelvin avait “ limité l’âge de la Terre à condition qu’aucune source nouvelle de chaleur ne soit découverte. Cette formulation prophétique désigne justement ce que nous examinons ce soir, le radium ! ” Et là, merveille ! Le visage du vieux bonhomme s’épanouit en un large sourire.
Attention, cette anecdote est sans doute à l’origine de l’idée que l’erreur de Kelvin résultait uniquement de son ignorance de la radioactivité, alors qu’on l’a vu le problème résidait surtout dans son refus de la convection mantellique. Il convient donc de garder à l’esprit que la déclaration de Rutherford visait uniquement à ménager la susceptibilité de son glorieux collègue.
Ensuite, les âges s’envolent. Qu’on en juge, en 1906 Robert Strutt attribue jusqu’à 2,4 milliards d’années à une roche ! Paradoxalement, ces durées immenses posent tout autant de difficultés aux géologues que ne le faisaient les datations trop courtes de Kelvin. En effet, leurs estimations des taux de sédimentation ou d’érosion indiquent plutôt des âges de quelques centaines de millions d’années. Il faudra trois décennies, entre 1911 et 1931, pour que les travaux menés par Arthur Holmes et Joseph Barrell, en mêlant les données issues de la radiochronologie et des autres chronomètres naturels (en particulier les taux de sédimentation), parviennent à assigner des âges qui fassent consensus aux différentes périodes géologiques. Du moins jusqu’au Précambrien, lequel est renvoyé au-delà de 600 millions d’années. Au-delà c’est l’inconnu, mais il ne fait plus guère de doute que l’âge de la Terre doit se chiffrer en milliard d’années.
Cependant, le chronomètre de Rutherford présente un défaut en apparence insurmontable : il permet de dater des roches terrestres, mais pas la planète elle-même. On obtient, au mieux, l’âge de la plus vieille roche découverte, sans jamais être certain qu’il n’en existe pas une autre plus ancienne. Et même en admettant que les roches originelles aient subsisté jusqu’à nous, elles seraient encore plus récentes que la Terre puisque celle-ci, dans sa prime jeunesse, était entièrement constituée de magma.
La fin de cette histoire est connue : des géochimistes vont se tourner vers la datation des météorites et en parvenant à estimer leur âge à 4,5 milliards d’années ils aboutiront à l’âge que l’on prête encore aujourd’hui à notre planète. Mais, cela n’a de sens qu’à la condition de supposer que la Terre a été formée par l’accrétion de ces astéroïdes qui croisent parfois notre orbite dans l’espace. D’où vient donc cette hypothèse ?
Elle remonte au XVIIIème siècle et à l’intuition d’un philosophe, Emmanuel Kant, dont l’un des premiers livres s’intitulait : Universal natural history and theory of the heavens (Histoire naturelle universelle et théorie du ciel). Autre siècle, autre mœurs. On retrouve donc dans cet ouvrage le vieil objectif d’élaborer une cosmogonie reposant sur le seul jeu des lois de la nature :
- Emmanuel Kant, Histoire naturelle générale et théorie du ciel, traduction française de 1886 (éd. originale 1755)
J’ai choisi un sujet qui peut paraître, à première vue, de nature à rebuter bon nombre de lecteurs par ses difficultés propres, et aussi parce qu’il semble froisser leurs sentiments religieux. Découvrir les lois systématiques qui relient les mondes créés dans l’étendue de l’espace infini, et déduire de l’état primitif de la nature, par les seules lois de la Mécanique, la formation des corps célestes et l’origine de leurs mouvements : une telle entreprise semble dépasser de beaucoup les forces de la raison humaine. D’autre part, la Religion menace de ses foudres l’audacieux qui oserait attribuer à l’action de la nature seule une œuvre où elle voit avec raison l’intervention immédiate de l’Être suprême, et elle craint de rencontrer dans la curiosité indiscrète d’une pareille tentative une apologie de l’athéisme. Je vois clairement la force de ces objections et pourtant je ne me laisse pas décourager. Je sens toute la puissance des obstacles qui se dressent devant moi, et je ne me laisse pas abattre. Sur la foi d’une simple conjecture, j’ai entrepris un dangereux voyage, et déjà j’aperçois les avancées de terres nouvelles ! Ceux qui auront le courage de poursuivre cette entreprise les atteindront et auront la gloire d’y attacher leur nom (préface).
Kant imagine tout simplement que le système solaire s’est formé à partir d’une nébuleuse :
Je suppose donc que tous les matériaux dont se composent les sphères, planètes et comètes, qui appartiennent à notre monde solaire, décomposés à l’origine des choses en leurs éléments primitifs, ont rempli alors l’espace entier dans lequel circulent aujourd’hui ces astres. Cet état de la nature, lorsqu’on le considère en soi et en dehors de toute préoccupation de système, paraît être le plus simple qui ait pu succéder au néant. A cette époque, rien n’avait encore pris une forme. La formation et le rassemblement de corps célestes isolés, séparés par des intervalles proportionnés aux attractions, leur forme qui résulte de l’équilibre de la matière amassée pour les produire, tout cela constitue un état postérieur de la nature (…) Dans un espace ainsi rempli, le repos ne dure qu’un instant. Les éléments possèdent par essence les forces qui peuvent les mettre en mouvement, et sont pour eux-mêmes sources de vie. La matière est par suite en effort constant pour se façonner. Les éléments disséminés d’espèce plus dense attirent à eux toute la matière plus légère qui les environne ; eux-mêmes, avec les matériaux qu’ils ont déjà ramassés, se réunissent dans les points où existent des particules d’espèce plus dense encore, ceux-ci à leur tour à d’autres plus denses et ainsi de suite. Et si l’on suit par la pensée ce travail de la nature à travers l’étendue du chaos, on voit aisément que la conséquence en sera la formation de diverses masses, qui, une fois créées, resteront éternellement en repos, équilibrées par l’égalité de leurs attractions mutuelles. Mais la nature tient en réserve d’autres forces, qui s’exercent particulièrement lorsque la matière est décomposée en très petites particules ; ces forces font que les particules se repoussent mutuellement, et par leur lutte incessante contre l’attraction, elles donnent naissance au mouvement, qui est la vie de la nature. Sous l’empire de cette force de répulsion, qui se manifeste dans l’élasticité des vapeurs, la diffusion des corps odorants et l’expansion de toute matière gazeuse, et qui est un phénomène incontestable de la nature, les éléments qui tombent vers les centres d’attraction abandonnent la direction rectiligne de leur mouvement, et leur chute verticale se transforme en des mouvements curvilignes autour du centre d’attraction (…) Ce corps, qui occupe le centre d’attraction, et qui va devenir le plus important du monde planétaire par la continuelle adjonction des matériaux qu’il attire, ce corps est le Soleil, bien qu’il n’ait pas encore l’éclat flamboyant qui se produira sur sa surface après sa complète formation (…) Si l’on examine maintenant cette matière élémentaire du monde en mouvement, dans l’état où elle a été amenée par l’attraction et par une suite mécanique des lois générales de la résistance, nous voyons un espace, compris entre deux plans peu éloignés l’un de l’autre et également distants du plan général d’attraction, qui, à partir du centre du Soleil, s’étend à des distances inconnues, et dans l’intérieur duquel toutes les particules, chacune en raison de sa distance et de l’attraction qui la gouverne, décrivent d’une course libre des orbites circulaires déterminées. Par suite, puisqu’une telle distribution est celle où elles se gênent mutuellement le moins possible, ces particules persisteront éternellement dans leur mouvement, à moins que l’attraction de ces particules de la matière primitive les unes sur les autres ne commence à faire sentir son action et ne produise de nouvelles formations qui seront les semences d’où naîtront les planètes. Car, puisque les éléments qui se meuvent en cercles parallèles autour du Soleil, pris à des distances du Soleil peu différentes, sont presque en repos relatif en raison de l’égalité de leurs mouvements parallèles, l’attraction des éléments ainsi placés, et doués d’une force attractive prépondérante, commence aussitôt à produire une action considérable : ils provoquent la réunion des particules les plus voisines pour en former un corps, qui, à mesure de l’accroissement de sa masse, étend de plus en plus sa sphère d’attraction, et met en mouvement pour s’augmenter les éléments de régions de plus en plus éloignées (p.149-153).
Le terme « nébuleuse » apparaît dans le premier chapitre de l’ouvrage :
Il n’y a pas à chercher longtemps dans les observations des astronomes pour rencontrer de semblables apparences. Elles ont été vues par divers observateurs. On s’est étonné de leur rareté ; on a imaginé sur leur compte et l’on a admis tantôt les fantaisies les plus étonnantes, tantôt des conceptions plus spécieuses, mais qui n’avaient pas plus de fondement que les premières. Nous voulons parler des nébuleuses, ou plus exactement d’une espèce particulière de ces astres, que M. de Maupertuis décrit ainsi : ce sont de petites plaques lumineuses, un peu plus brillantes seulement que le fond obscur du ciel ; elles se présentent dans toutes les régions ; elles offrent la figure d’ellipses plus ou moins ouvertes ; et leur lumière est beaucoup plus faible que celle d’aucun autre objet que l’on puisse apercevoir dans le ciel (…) M. de Maupertuis, les tient, en raison de leur figure et de leur diamètre apparent sensible, pour des corps célestes d’une grandeur énorme, fortement aplatis par suite d’une rotation rapide et qui, vus obliquement, offrent la forme ovale (p.139-140).
Mais, Kant se trompe quant à leur composition puisqu’il y voit une réunion de nombreux soleils :
On reconnaîtra aisément que cette dernière explication ne peut être acceptée. Puisque ces nébuleuses sont certainement au moins aussi éloignées de nous que les étoiles fixes, il ne suffirait pas de leur supposer une grandeur prodigieuse, qui surpasserait des milliers de fois celle des plus grosses étoiles : il faudrait ensuite expliquer par quel paradoxe ces corps, qui sont des soleils lumineux par eux-mêmes, nous paraissent, malgré leurs étonnantes dimensions, comme les plus faibles et les plus pâles de tous les astres. Il est bien plus naturel et raisonnable de supposer qu’une nébuleuse n’est pas un unique et énorme soleil, mais un système de nombreux soleils, rassemblés en raison de leur distance dans un espace si étroit, que leur lumière, qui serait imperceptible pour chacun d’eux isolément, parvient, grâce à leur innombrable quantité, à produire une blancheur pâle et uniforme. L’analogie avec le système d’étoiles dont nous faisons partie, leur forme qui est exactement celle qu’ils doivent avoir dans notre théorie, la faiblesse de leur lumière qui dénote un éloignement infini, tout concorde admirablement pour nous faire prendre ces taches elliptiques pour des mondes ordonnés comme le nôtre, en un mot, pour des Voies lactées semblables à celle dont nous avons expliqué la constitution (p.140)
C’est le physicien et astronome Pierre-Simon de Laplace qui en 1796 va faire le lien entre les nébuleuses et la théorie de l’accrétion planétaire formulée par Kant. Il commence par réfuter la cosmogonie de Buffon :
- Pierre-Simon de Laplace, Exposition du système du monde, 1796*
On a, par le Chapitre précédent, pour remonter à la cause des mouvements primitifs du système planétaire, les cinq phénomènes suivants : les mouvements des planètes dans le même sens et à peu près dans un même plan ; les mouvements des satellites dans le même sens que ceux des planètes ; les mouvements de rotation de ces différents corps et du Soleil, dans le même sens que leurs mouvements de projection et dans des plans peu différents ; le peu d’excentricité des orbes des planètes et des satellites ; enfin, la grande excentricité des orbes des comètes, quoique leurs inclinaisons aient été abandonnées au hasard. Buffon est le seul que je connaisse, qui, depuis la découverte du vrai système du monde, ait essayé de remonter à l’origine des planètes et des satellites. Il suppose qu’une comète, en tombant sur le Soleil, en a chassé un torrent de matière qui s’est réuni au loin, en divers globes plus ou moins grands et plus ou moins éloignés de cet astre ; ces globes, devenus par leur refroidissement opaques et solides, sont les planètes et leurs satellites. Cette hypothèse satisfait au premier des cinq phénomènes précédents ; car il est clair que tous les corps ainsi formés doivent se mouvoir à peu près dans le plan qui passait par le centre du Soleil et par la direction du torrent de matière qui les a produits : les quatre autres phénomènes me paraissent inexplicables par son moyen. (…) Un phénomène, non seulement très difficile à expliquer dans cette hypothèse, mais qui lui est contraire, est le peu d’excentricité des orbes planétaires. On sait par la théorie des forces centrales que, si un corps mû dans un orbe rentrant autour du Soleil rase la surface de cet astre, il y reviendra constamment à chacune de ses révolutions ; d’où il suit que, si les planètes avaient été primitivement détachées du Soleil, elles le toucheraient à chaque retour vers cet astre, et leurs orbes, loin d’être circulaires, seraient fort excentriques. Il est vrai qu’un torrent de matière, chassé du Soleil, ne peut pas être exactement comparé à un globe qui rase sa surface ; l’impulsion que les parties de ce torrent reçoivent les unes des autres et l’attraction réciproque qu’elles exercent entre elles peuvent, en changeant la direction de leurs mouvements, éloigner leurs périhélies du Soleil. Mais leurs orbes devraient toujours être fort excentriques, ou du moins ils n’auraient pu avoir tous de petites excentricités que par le hasard le plus extraordinaire (p.498-499).
*cet extrait se trouve dans une note additionnelle qui ne figure pas dans les premières éditions. Je le rapporte ici à partir de la sixième édition publiée en 1835.
Puis, Laplace décrit un phénomène d’accrétion planétaire assez proche de celui que l’on conçoit encore aujourd’hui :
Pour leur avoir donné dans le même sens un mouvement presque circulaire autour du Soleil, il faut que ce fluide ait environné cet astre comme une atmosphère. La considération des mouvements planétaires nous conduit donc à penser qu’en vertu d’une chaleur excessive, l’atmosphère du Soleil s’est primitivement étendue au delà des orbes de toutes les planètes, et qu’elle s’est resserrée successivement jusqu’à ses limites actuelles. Dans l’état primitif où nous supposons le Soleil, il ressemblait aux nébuleuses que le télescope nous montre composées d’un noyau plus ou moins brillant, entouré d’une nébulosité qui, en se condensant à la surface du noyau, le transforme en étoile. Si l’on conçoit, par analogie, toutes les étoiles formées de cette manière, on peut imaginer leur état antérieur de nébulosité précédé lui-même par d’autres états dans lesquels la matière nébuleuse était de plus en plus diffuse, le noyau étant de moins en moins lumineux. On arrive ainsi, en remontant aussi loin qu’il est possible, à une nébulosité tellement diffuse, que l’on pourrait à peine en soupçonner l’existence (…) Mais comment l’atmosphère solaire a-t-elle déterminé les mouvements de rotation et de révolution des planètes et des satellites ? Si ces corps avaient pénétré profondément dans cette atmosphère, sa résistance les aurait faite tomber sur le Soleil ; on peut donc conjecturer que les planètes ont été formées à ces limites successives, par la condensation des zones de vapeurs, qu’elle a dû, en se refroidissant, abandonner dans le plan de son équateur (…) Si toutes les molécules d’un anneau de vapeurs continuaient de se condenser sans se désunir, elles formeraient à la longue un anneau liquide ou solide. Mais la régularité que cette formation exige dans toutes les parties de l’anneau et dans leur refroidissement a dû rendre ce phénomène extrêmement rare. Aussi le système solaire n’en offre-t-il qu’un seul exemple, celui des anneaux de Saturne. Presque toujours chaque anneau de vapeurs a dû se rompre en plusieurs masses qui, mues avec des vitesses très peu différentes, ont continué de circuler à la même distance autour du Soleil. Ces masses ont dû prendre une forme sphéroïdique, avec un mouvement de rotation dirigé dans le sens de leur révolution, puisque leurs molécules inférieures avaient moins de vitesse réelle que les supérieures ; elles ont donc formé autant de planètes à l’état de vapeurs. Mais si l’une d’elles a été assez puissante pour réunir successivement par son attraction toutes les autres autour de son centre, l’anneau de vapeurs aura été ainsi transformé dans une seule masse sphéroïdique de vapeurs, circulant autour du Soleil, avec une rotation dirigée dans le sens de sa révolution. Ce dernier cas a été le plus commun (p.499-502).
La théorie de Laplace pose plusieurs problèmes d’astrophysique, en particulier parce qu’elle n’explique pas la répartition du moment cinétique entre le Soleil et les planètes. Cela a entraîné le développement de diverses théories similaires, mais plus ou moins modifiées, au cours du XXème siècle. Par exemple en 1904 Thomas Chamberlin et Forest Moulton formulent la théorie des planétésimaux dans laquelle l’accrétion se déroule à froid à partir d’astéroïdes. Elle-même fut ensuite abandonnée. Néanmoins, l’idée qui nous intéresse, à savoir la formation des planètes à partir de l’accrétion de planétésimaux, a été conservée.
Reste à trouver une méthode fiable de datation radiochronologique. Celle-ci commence à se dessiner lorsqu’en 1913, Frededick Soddy découvre le concept d’isotopes. Ainsi, il n’existe pas une mais plusieurs sortes d’uranium, de thorium ou encore de plomb. Au cours des deux décennies qui suivent on parvient à démêler plusieurs chaînes de désintégration radioactives montrant ainsi que :
– la désintégration de l’uranium 238 aboutit à la formation de plomb 206
– la désintégration de l’uranium 235 aboutit à la formation de plomb 207
– la désintégration du thorium 232 aboutit à la formation de plomb 208
Entre 1936 et 1941, Alfred Nier introduit l’utilisation d’un nouvel appareil, le spectromètre de masse qui lui permet de déterminer la quantité de chaque isotope dans un échantillon. Cela lui fera dire avec beaucoup de poésie : « n’oubliez pas que pour dater la Terre il a fallu peser des atomes ». Ainsi, se constitue la méthode plomb/plomb dont la fiabilité repose sur sa capacité à croiser les âges obtenus via trois chaînes de désintégrations différentes. Et ses résultats sont surprenants : le minéral le plus vieux daté de cette façon affiche plus de 2,2 milliards d’années, à tel point que Nier se demande s’il ne s’est pas trompé parce qu’il pense la Terre moins âgée que son échantillon.
Mais, cette méthode est encore imparfaite car elle ne corrige pas la présence de plomb radiogénique au moment de la formation du minéral. Au lendemain de la seconde guerre mondiale, le physicien allemand Friedrich Houtermans trouve la solution : il suffit de considérer l’évolution du rapport entre le plomb radiogénique (en l’occurrence 206Pb et 207Pb) et un isotope stable de cet élément le plomb 204. Au cours du temps, la teneur en plomb radiogénique augmente tandis que celle du 204Pb ne varie pas. Ce dernier se « dilue » ainsi progressivement au milieu des isotopes radiogéniques. Mais, surtout, ce phénomène est proportionnel à la quantité d’uranium présente initialement dans l’échantillon : plus il y en a plus la « dilution » est rapide puisque l’uranium donne naissance à du plomb radiogénique. Houtermans découvre alors que les rapports isotopiques des minéraux qu’il étudie s’alignent sur une droite isochrone dont la pente donne l’âge avec un haut degré de confiance.
La suite de l’histoire se déroule aux USA. En 1953, Clair Patterson étudie plusieurs météorites dont celle du cratère de Canyon diablo. Cette dernière renferme des minéraux très pauvres en uranium et en thorium, pourtant le 204Pb s’y trouve fortement « dilué ». En fait, Patterson n’a jamais observé une telle dilution ce qui le conduit à supposer que cette météorite est très ancienne. Il n’imagine pas à quel point. Lorsqu’il communique ses résultats à Houtermans celui-ci applique la méthode plomb/plomb et annonce 4,5 milliards d’années. Afin d’en avoir le cœur net, Patterson multiplie les mesures sur d’autres météorites qui toutes s’alignent sur la droite isochrone de Canyon diablo. Il décide alors de comparer ces résultats aux rapports isotopiques du plomb dans les sédiments marins. Une idée lumineuse car ce plomb provient de l’érosion continentale qui en drainant de vastes surfaces offre finalement un mélange très représentatif du plomb primordial et du plomb radiogénique terrestre. Et ce mélange se positionne lui aussi sur la droite isochrone. Le doute n’est plus permis. Le 21 janvier 1955, Clair Patterson publie ses résultats dans la revue Science en compagnie de deux collaborateurs George Tilton et Mark Inghram. L’article s’intitule bien évidemment Age of the earth.
Depuis 1955, de nombreuses autres méthodes de datations, fondées sur les progrès de la géochimie, des modèles cosmologiques ainsi que de l’étude des roches lunaires et martiennes, ont toutes confirmé l’ordre de grandeur de l’estimation de Patterson : la Terre est âgée d’un peu plus de 4500 millions d’années. La variation des résultats ne porte plus que sur le nombre de dizaines associé à cet âge. Bien sûr, la Science ne produit pas de vérité absolue et nul ne peut prétendre que cette datation ne sera jamais remise en question. Néanmoins, le fait qu’elle ait résisté à des tests aussi nombreux que variés pendant plus d’un demi-siècle, témoigne du haut de gré de confiance qu’il nous est permis de lui accorder.
BIBLIOGRAPHIE DES SOURCES CONTEMPORAINES
LIVRES
Stephen Jay Gould, Aux racines du temps, 1987
François Ellenberger, Histoire de la géologie, 1988 (tome 1), 1994 (tome 2)
Jacques Roger, édition critique des Époques de la Nature, 1988
Gabriel Gohau, Les sciences de la Terre au XVIIe et XVIIIe siècles, naissance de la géologie, 1990
Jacques Roger, Pour une histoire des sciences à part entière, 1995
Pascal Richet, L’âge du monde, 1999
Vincent Deparis et Hilaire Legros, Voyage à l’intérieur de la Terre, 2000
Gabriel Gohau, Naissance de la géologie historique, 2003
Sandra Herbert, Charles Darwin, Geologist, 2005
André Pichot, Expliquer la vie, 2011
ARTICLES
Gabriel Gohau, Le temps long des « catastrophistes », in Travaux du comité français d’histoire de la géologie, 1980
Jacques Roger, La place de Buffon dans l’histoire des Sciences de la Terre, in Travaux du comité français d’histoire de la géologie, 1988
Philip England, Peter Molnar et Frank Richter, Kelvin, Perry et l’âge de la Terre, in Pour La Science n°364, 1999
Gabriel Gohau, Thomas Burnet, la première théorie de la Terre : entre science et religion, in Travaux du comité français d’histoire de la géologie, 2000
Pierre Thomas, Pourquoi la mer est-elle salée ? in Planet Terre ENS Lyon, 2001
Francis Albarède, Pourquoi la mer est-elle salée ? in Planet Terre ENS Lyon, 2001
Bernard Bourdon, Les âges de la Terre, in Dossier Pour la Science n°42, 2004
Philip England, Peter Molnar et Frank Richter, Kelvin, John Perry’s neglected critique of Kelvin’s age for the Earth: A missed opportunity in geodynamics, in Geological Society of America, 2007
Jean-Michel Yvard, Géologie, théologie et inquiétudes eschatologiques : William Thomson (Lord Kelvin) et les débats suscités par la thermodynamique à l’époque victorienne, in Actes du colloque de la S.F.E.V.E. à l’université de Provence, 2008
Gabriel Gohau, Darwin géologue, entre Lyell et Humboldt, in Travaux du comité français d’histoire de la géologie, 2009
Hubert Krivine, Histoire de l’âge de la Terre, in images de la physique, 2011
Nadia Pizanias, Géologie et religion au XIXe siècle en Europe occidentale : la question du déluge, in Travaux du comité français d’histoire de la géologie, 2013
Colette Le Lay et Frédérique Rémy, Dissertation sur la glace, in Revue d’histoire des sciences, 2015
Pierre Savaton, Le temps fondateur de la géologie, in Romantisme, 2016
Pierre Thomas, Buffon, ou comment le siècle des Lumières envisageait l’origine du monde, in Planet Terre ENS Lyon, 2012
Pierre Thomas, L’histoire de l’âge de la Terre, in Planet Terre ENS Lyon, 2020

