par Philippe Cosentino
Que ce soit dans l’enseignement de spécialité (lien), ou en enseignement scientifique de tronc commun (lien), le modèle théorique de population de Hardy Weinberg fait son entrée dans les programmes de terminale.
Extrait du programme d’enseignement scientifique :
Le modèle mathématique de Hardy-Weinberg (…) prédit que la structure génétique d’une population de grand effectif est stable d’une génération à l’autre sous certaines conditions (absence de migration, de mutation et de sélection). (…) Les écarts entre les fréquences observées sur une population naturelle et les résultats du modèle s’expliquent notamment par les effets de forces évolutives (mutation, sélection, dérive, etc.).
Ce modèle correspond à une population idéale, panmictique, où l’effectif serait infini, où il n’y aurait ni mutations, ni migrations, ni sélection.
Dans ce modèle de référence, on peut démontrer mathématiquement (en partant d’un échiquier de croisement par exemple) que :
- les fréquences alléliques ne varient pas d’une génération à l’autre
- les fréquences des génotypes peuvent être prédits à partir des fréquences alléliques : f(A//A) = f(A)² , f(A//B) = 2 f(A).f(B) etc.
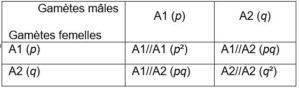
S’il y a panmixie etc. alors on peut déduire la fréquence des génotypes de la génération suivante à partir de celle des allèles
Si dans une population réelle, on observe d’importantes variations temporelles des fréquences alléliques, et/ou un fort écart entre les fréquences génotypiques prédites et observées, cela signifie qu’une des conditions du modèle n’est pas respecté (soit l’effectif est trop réduit, soit il y a sélection etc.).
Nous proposons une activité de modélisation qui se donne pour objectif de vérifier que plus l’effectif d’une population est faible, plus les fréquences alléliques fluctueront, et plus les fréquences génotypiques observées seront éloignées des fréquences prédites par le calcul.
Présentation du logiciel
L’application “dérive diploïde” a déjà fait l’objet d’un article sur ce site (lien).
A noter : cette application peut être utilisée sur les tablettes de la région, et donc faire l’objet d’une activité en classe entière, dans une salle banalisée.
Cependant, si l’application permettait déjà à l’époque de suivre l’évolution des fréquences alléliques, elle ne permettait pas encore de suivre celle des fréquences génotypiques. On ne pouvait ainsi pas l’utiliser dans le cadre de l’étude du modèle de Hardy-Weinberg.
Depuis, l’auteur a rajouté cette possibilité, qui n’apparaît que lorsque le nombre d’allèles choisi au démarrage est égal à 2 (cela n’aurait pas de sens d’utiliser la formule p² + 2pq + q² = 1 avec 3 allèles).
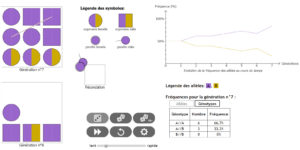
En sélectionnant un nombre initial d’allèles égal à 2, le logiciel offre la possibilité de choisir la fréquence initiale du 1er allèle. Par la suite il permettra également de suivre la fréquence des génotypes.
Une fois le nombre d’allèles fixé à 2, et la fréquence initiale choisie, l’utilisateur valide en cliquant sur OK.
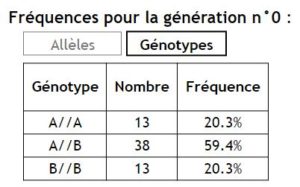
Un tableau permet, en bas à droite de l’écran, de suivre non seulement la fréquence des allèles mais aussi celle des génotypes.
Après avoir sélectionné “génotypes”, le tableau affiche la fréquence des 3 différents génotypes.
Pour le reste, le fonctionnement est inchangé. On peut faire se reproduire les individus soit un couple à la fois, soit, pour aller plus vite, passer directement à la génération suivante. Une fiche technique (lien) rappelle les principales fonctionnalités du logiciel.
Si l’effectif est élevé, on constate que les fréquences des allèles fluctuent peu, et que les fréquences des génotypes observés restent proches de ceux que l’on peut prédire par le calcul à partir de la fréquence des allèles (en supposant que la population s’approche du modèle de Hardy-Weinberg).
Avec un effectif faible, les fréquences fluctuent énormément, à tel point qu’au bout d’un certain nombre de générations un allèle peut disparaître (dérive génétique). Les fréquences des génotypes quant à elles, sont souvent très éloignées de celles que l’on peut prédire à partir du modèle de Hardy-Weinberg.
Avec un effectif faible, les fréquences alléliques fluctuent considérablement (dérive génétique)
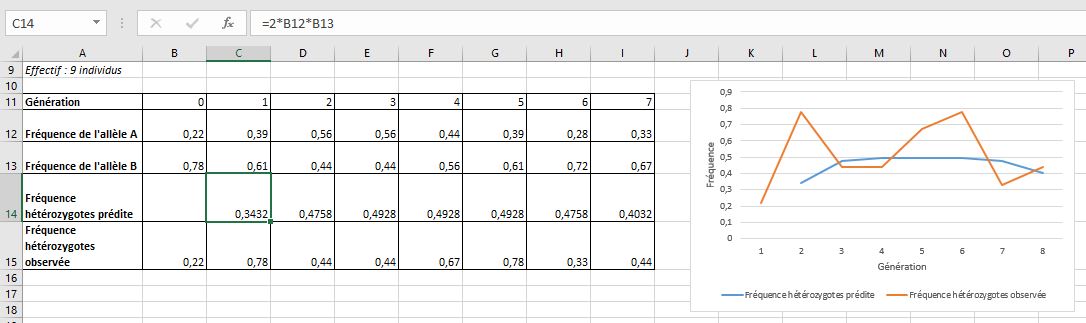
Pour simplifier l’étude, on peut se limiter au cas des hétérozygotes, et suivre par exemple, dans un tableau, l’évolution dans le temps des fréquences prédites (par la relation 2.p.q) et des fréquences observées.
La capture d’écran ci-dessous présente le détail d’un tableau obtenu avec un effectif de 9 individus. Le détail du calcul de la fréquence prédite pour les hétérozygotes apparaît en haut de l’écran.
Résultats obtenus avec 9 individus pour une fréquence initiale p=0,2
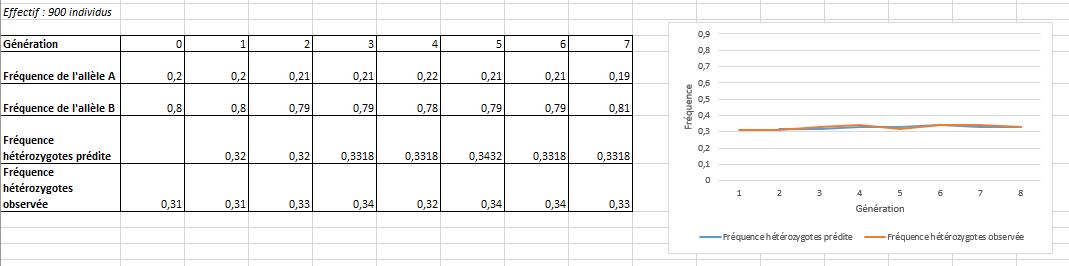
Avec 900 individus, les fréquences alléliques et génotypiques sont quasiment constantes d’une génération à la suivante.
De plus, les fréquences génotypiques observées sont très proches des fréquences génotypiques observées. On a bien mis en évidence une relation entre l’effectif, la fluctuation, et la conformité des fréquences prédites et observées.
Résultats observés avec 900 individus
Liens
Lien vers l’application :
https://www.pedagogie.ac-nice.fr/svt/productions/derive-diplo/index.htm
Lien vers l’article décrivant “Dérive diploïde” :
https://www.pedagogie.ac-nice.fr/svt/?p=556
Programme d’enseignement scientifique de terminale :
https://cache.media.eduscol.education.fr/file/SPE8_MENJ_25_7_2019/84/7/spe241_annexe_1158847.pdf
Programme de spécialité SVT de terminale :
https://cache.media.eduscol.education.fr/file/SPE8_MENJ_25_7_2019/11/4/spe252_annexe_1159114.pdf
